6. Quantizzazione
Iniziamo ora ad affrontare il problema della quantizzazione, partendo da un esercizio: un fotone di energia E deve attraversare due beam splitter distanti tra di loro una distanza L. L'elettrone ha il 50% di probabilità di venire trasmesso o riflesso da ognuno dei beam splitter, mentre la sua ampiezza subisce uno sfasamento di p ogni volta che viene riflesso; è possibile calcolare la probabilità che superi i due beam splitter?
Chiamando i beam splitter A e B come in Figura 25, si possono individuare infiniti cammini attraverso cui il fotone può arrivare dalla sorgente al rivelatore: quello principale è Sorgente-A-B-Rivelatore; ma vi sono anche Sorgente-A-B-A-B-Rivelatore, Sorgente-A-B-A-B-A-B-Rivelatore, e in generale tutti quelli che si ottengono aggiungendo un numero arbitrario di giri completi B-A-B. La differenza di fase tra cammini successivi è quindi, contando la perdita di fase dovuta alle riflessioni, .
Siccome la probabilità di rivelare il fotone a ciascuna delle due uscite di un beam splitter è del 50% (0.5), i vettori ampiezza dei cammini trasmesso e riflesso vanno entrambi moltiplicati, dopo la trasmissione o la riflessione, per , cioè il loro modulo si riduce. In precedenza abbiamo ignorato questo fatto, perché i cammini che consideravamo subivano tutti lo stesso numero di trasmissioni e riflessioni, ma ora non è più così: sommiamo su cammini che hanno un diverso numero di riflessioni e trasmissioni, e quindi sommiamo vettori di lunghezza diversa. Questo rende difficile ottenere la probabilità di rivelazione con una formula, ma non impedisce di trovare quei valori dell'energia del fotone per cui la probabilità di trasmissione è massima. Infatti, la condizione di massimo è verificata se la differenza di fase tra due cammini successivi è un multiplo dell'angolo giro. Quindi si avrà tale condizione per:
|
|
(26) |
Poiché per il fotone
|
|
(27) |
Si trova, sostituendo la (27) nella (26):
|
|
(28) |
Esiste quindi un insieme discreto di valori dell'energia del fotone per cui la probabilità di trasmissione è massima. Anche in questo caso una simulazione realizzata con GeoGebra (Figura 25) può aiutare a visualizzare il problema proposto (disponibile anche al link https://tube.geogebra.org/material/simple/id/oiwrDPnR).
Figura 25. Simulazione del problema della probabilità di trasmissione tra due barriere "risonanti". La simulazione permette di risolvere il problema sia nel caso del fotone, appena trattato, sia nel caso dell'elettrone, discusso nel seguito. Le simulazioni nei due casi non vanno considerate nella stessa scala (sono costruite ponendo sia la velocità della luce sia la massa dell'elettrone pari ad 1).
Cosa cambia nel problema precedente se anziché un fotone prendiamo in considerazione un elettrone, e quindi sostituiamo i beam splitter con barriere di potenziale capaci di riflettere o trasmettere l'elettrone con una probabilità in entrambi i casi del 50%? Non molto, infatti il ragionamento resta analogo, così come continua a valere l'equazione (26) per la differenza di fase tra due cammini successivi. Cambia però la relazione tra il numero d'onda dell'elettrone e la sua energia, che diventa
|
|
(29) |
Dove m è la massa dell'elettrone. Sostituendo ora la (29) nella (27) si trova:
|
|
(30) |
Anche in questo caso la probabilità che l'elettrone oltrepassi le due barriere risulta massima in corrispondenza di ben determinate energie, dipendenti dalla distanza tra le barriere. La differenza tra la formula (28) e la (30) spiega la principale differenza che si riscontra nella simulazione di Figura 25 quando viene utilizzato un fotone oppure un elettrone: nel primo caso i picchi di trasmissione si ritrovano a valori di energia equispaziati (proporzionali ai numeri interi) mentre nel secondo caso tali valori non sono equispaziati (proporzionali ai quadrati dei numeri interi).
Verso la quantizzazione: due beam splitter o due barriere di potenziale semitrasparenti sono in grado di selezionare le energie degli oggetti quantistici (fotoni o particelle massive) che cercano di attraversarle. La probabilità di attraversamento è massima per alcune energie di risonanza, che dipendono dalla distanza tra le due barriere.
6.1. Elettrone in una “scatola”
Poniamoci invece nel caso di un elettrone confinato in una “scatola” unidimensionale di larghezza L, cioè in una buca di potenziale di altezza infinita, elettrone che non può quindi fuggire dalla regione di spazio in cui è intrappolato; denominiamo gli estremi della scatola con le lettere A e B (vedi Figura 26).
Si vuole valutare la probabilità che l'elettrone originariamente nella posizione S venga rivelato da un rivelatore posto in D. Come per i fotoni, i cammini da S a D che includono una riflessione su una parete della buca vedono la fase del fasore associato diminuire di p.
Anche in questo caso, abbiamo un'infinità di cammini possibili, riuniti questa volta in quattro famiglie. I quattro cammini possibili di base da S a D sono: quello diretto (cammino da S a D), riflessione dall'estremo B (cammino SBD), riflessione dall'estremo A (cammino SAD) e riflessione da entrambe le pareti, partendo verso sinistra (cammino SABD). Tutti gli altri cammini possibili si ottengono da questi quattro cammini di base, assumendo che l'elettrone prima di arrivare in R sia tornato nella posizione di partenza S con due riflessioni dalle pareti della scatola (partendo verso destra), quindi con una o più ripetizioni del cammino SBAD.
La fase dei vettori corrispondenti ai quattro cammini principali dipenderà dalla posizione di S ed R all'interno della barriera; ma la differenza di fase tra due cammini successivi della stessa famiglia no: sarà infatti
|
|
(31) |
Cioè identica a quella esaminata nell'esercizio precedente. Si può quindi ragionare in modo simile al problema della trasmissione da due barriere: i massimi di probabilità di rivelazione si avranno per quei valori dell'energia che rendono la differenza di fase tra due cammini successivi pari a un multiplo intero di 2 π. In definitiva, le energie per le quali la probabilità è massima saranno le stesse di quelle calcolate nell'equazione (30):
|
|
(32) |
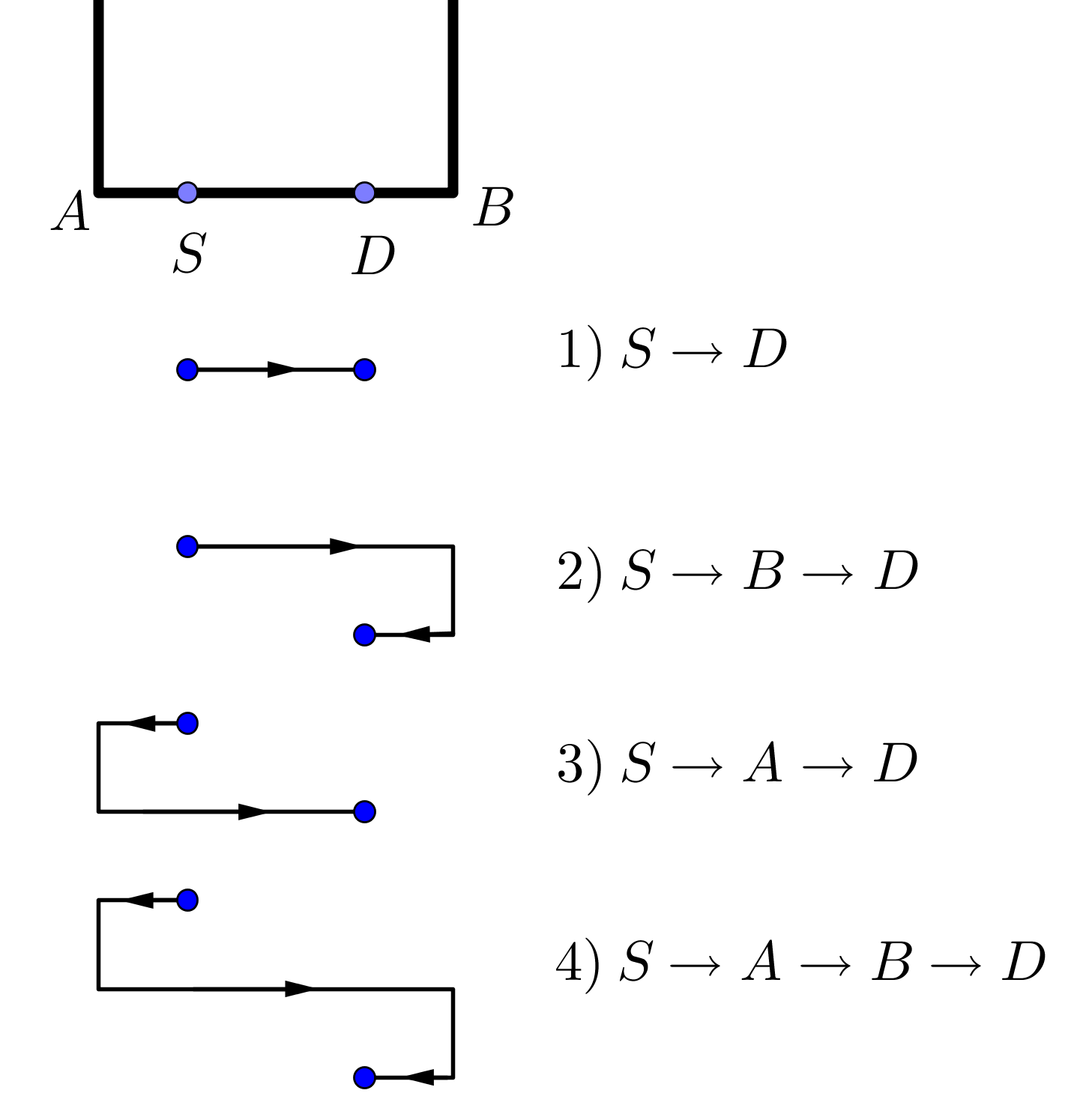
Figura 26. Schema delle famiglie di cammini possibili per l'elettrone confinato in una buca di potenziale infinita.
In realtà, poiché i cammini da considerare sono infiniti, e i vettori ad essi associati hanno tutti lunghezza unitaria (l'elettrone non può uscire dalla scatola, quindi anche se riflessi i vettori non subiscono alcuna attenuazione), l'ampiezza risultante per i valori dell'energia dati dall'equazione (32) sarà infinita. Cosa succede se l'energia non ha uno dei valori dell'equazione (32)? In questo caso la differenza di fase tra due cammini successivi della stessa famiglia è un angolo fissato, non multiplo di 2 π. Facendo la somma di tali ampiezze, dopo un certo numero di cammini la somma si annullerà. Nel limite in cui gli infiniti cammini vengono considerati tutti, solo per le energie permesse dall'equazione (32) vi sarà una probabilità di rivelare l'elettrone; per tutti gli altri valori, l'ampiezza, e quindi la probabilità, sarà nulla.
Ancora una volta una simulazione può aiutare a chiarire quanto abbiamo affermato (Figura 27 e link https://tube.geogebra.org/material/simple/id/Bo5umtmk). In essa si possono osservare dei “picchi” molto definiti per la probabilità di rivelazione, corrispondenti ai valori permessi dell'energia. Si può inoltre vedere che, per tutti gli altri valori, i vettori corrispondenti ai vari cammini si sommano distruttivamente e l'ampiezza risultate è molto piccola. La simulazione prende in considerazione solo 15 cammini per ciascuna famiglia, ma aumentando tale numero le righe si fanno sempre più nette, cioè la probabilità tende a diventare diversa da zero solo in corrispondenza ai valori di energia dati dalla (32).
Un oggetto quantistico confinato in uno spazio finito può avere perciò solo valori discreti dell'energia; e se in laboratorio si ha a disposizione un sistema simile, e si misura la sua energia, si potrà ottenere come risultato solo uno di tali valori. Noi abbiamo calcolato il livelli di energia ammessi per la “scatola”, cioè la buca di potenziale rettangolare infinita. Un oggetto quantistico potrebbe essere confinato da un potenziale di altro tipo, ad esempio di forma parabolica (come se fosse attirato verso un punto da una forza di tipo elastico). In questi casi i valori ammessi dell'energia saranno diversi, ma rimarrà la conclusione generale che solo un insieme discreto di valori dell'energia saranno ammessi.
Figura 27. Simulazione di un'elettrone confinato in una "scatola". È mostrata la probabilità di rivelazione in funzione dell'energia. Si notino i picchi, e, nella finestra di destra, i fasori che si sommano distruttivamente in corrispondenza di un valore dell'energia non permesso.
Quantizzazione: un elettrone confinato in una regione di spazio lunga L ammette solo alcuni valori discreti dell'energia come possibili, dipendenti dalla lunghezza. L'energia risulta quantizzata
6.2. L'energia nulla non è ammessa
Esaminando la formula (32) per le energie ammesse, notiamo che l'energia nulla non è ammessa, poiché l'indice n deve essere maggiore od uguale a zero. Questo è un risultato molto importante, che si può anche far risalire al principio di indeterminazione: se l'elettrone è confinato in uno spazio L, allora l'incertezza sulla posizione è pari a L/2. Per il principio di indeterminazione tra posizione e quantità di moto (equazione (22)):
|
|
(33) |
D'altronde, abbiamo che , quindi la media dell'energia sarà pari a:
|
|
(34) |
Applicando la formula statistica secondo la quale la media del quadrato di una variabile aleatoria è pari al quadrato della media più lo scarto quadratico medio
|
|
(35) |
e tenendo conto che il valor medio della quantità di moto è nullo,
|
|
(36) |
si ha che l'energia cinetica media dell'oggetto quantistico non può essere zero.
È interessante notare come il valore minimo dell'energia derivato tramite il principio di indeterminazione corrisponda esattamente al valore minimo dell'energia dato dall'equazione (32) . Questo non è vero per ogni potenziale mediante cui è possibile confinare un oggetto quantistico, ma in generale usando il principio di indeterminazione si può dare una stima ragionevole della minima energia possibile per quel potenziale, detta anche “energia dello stato fondamentale”.
L'energia nulla non è ammessa: l'elettrone (o qualunque oggetto quantistico) confinato in una “scatola” non ammette l'energia nulla tra le energie possibili, ma deve avere un'energia minima non nulla. Il principio di indeterminazione nega la possibilità che un oggetto quantistico rimanga fermo in una regione di spazio ben delimitata, e questo comporta che la sua energia non possa esser nulla.
6.3. Quantizzazione del momento angolare
Se si confina un elettrone su un anello circolare (Figura 28), si ottiene una situazione molto simile a quella appena esaminata della scatola, con alcune differenze.
Innanzitutto, nella scatola non è possibile distinguere i cammini che procedono verso sinistra da quelli orientati verso destra, perché la riflessione dalle pareti cambia il verso del moto. Di contro, un anello non ha riflessioni, e ciò rende i cammini con verso orario distinguibili da quelli con verso antiorario; quindi possiamo limitarci ad esaminare uno solo dei due casi.
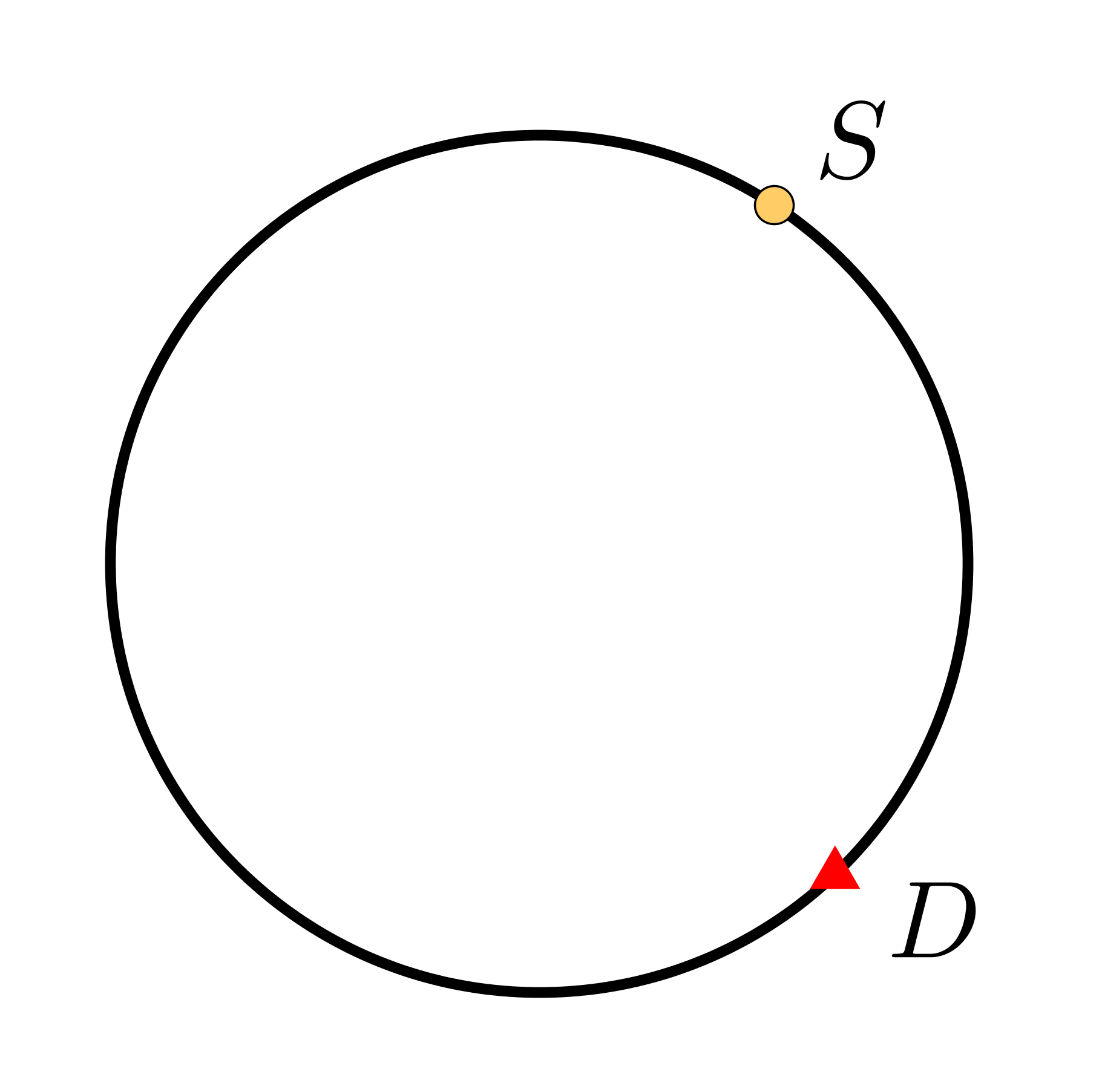
Figura 28. Schema del problema dell'oggetto quantistico confinato su un anello.
I cammini possibili per un determinato senso di rotazione si ottengono dal cammino diretto da S a D aggiungendo rotazioni complete nel verso desiderato. La differenza di fase tra cammini successivi diventa quindi . Si noti come l'assenza di riflessioni rimuove il termine sottrattivo 2p. Anche in questo caso affinché la probabilità finale non sia nulla i vettori corrispondenti a due cammini che differiscono di un giro completo devono essere paralleli, quindi la differenza di fase deve essere un multiplo intero di 2p. Da questa condizione si ottiene, ricordando ancora una volta che :
|
|
(37) |
E quindi, indicando con L il momento angolare dell'elettrone,
|
|
(38) |
Si può immediatamente notare come L risulti quantizzato, e non dipenda dal raggio dell'anello. Il momento angolare non può quindi assumere valori arbitrari, ma solo multipli interi (compreso lo zero) di una unità di momento angolare fondamentale ; questo risultato, ottenuto per un oggetto quantistico confinato in un anello circolare, è applicabile a tutti i moti di rotazione, anche diversi da quello circolare.
Anche l'energia risulta quantizzata, ma i valori non sono indipendenti dal raggio dell'anello. In particolare,
|
|
(39) |
In questo caso, il valore è ammesso. Quindi nel caso molto particolare del confinamento su un anello, è possibile che l'oggetto quantistico abbia energia nulla.
Quantizzazione del momento angolare: come per il caso dell'energia di una particella confinata in una scatola, anche il momento angolare risulta quantizzato, potendo assumere solo valori che risultino essere multipli interi di h/2p. Questi valori non dipendono dalla geometria del sistema.