2. Il modello di Feynman

Iniziamo ora la descrizione matematica del comportamento degli oggetti quantistici dovuta a Feynman. Innanzitutto, si deve entrare nell'ordine di idee che l'unica maniera per sapere dov'è un oggetto quantistico è rivelarlo. Nei problemi che riguardano fotoni avremo quindi tipicamente una sorgente in grado di emettere fotoni, e uno o più rivelatori (che generalmente considereremo ideali, ossia con efficienza 100%) in grado di rivelare la presenza del fotone in quel punto.

Il modello di Feynman si basa su un concetto fondamentale: nel cammino da sorgente a rivelatore, non si può assumere che il fotone percorra una singola traiettoria ben definita, ma occorre invece considerare tutti i possibili cammini tra la sorgente ed il rivelatore, cammini che devono però essere compatibili con i vincoli del sistema; ad esempio, la presenza di uno schermo impedisce al fotone di percorrere cammini che passino attraverso le parti opache di tale schermo.

Ogni cammino contribuisce alla probabilità che il fotone arrivi al rivelatore nel seguente modo: associamo ad ogni possibile cammino un'ampiezza o fasore; l'ampiezza è un vettore di lunghezza unitaria, il cui angolo di fase $φ$ varia lungo il cammino (con l'effetto di far “ruotare” il vettore) seguendo regole identiche a quelle di propagazione di un'onda classica: $φ = k x - ω t$ , dove x è la lunghezza del cammino, t è il tempo trascorso e $k = 2 π / λ$ è il numero d'onda.

Una volta calcolati i vettori associati a tutti i cammini possibili, l'ampiezza finale è pari alla somma vettoriale di tutti questi vettori. La probabilità di rivelare il fotone è proporzionale al quadrato del modulo dell'ampiezza finale. La probabilità effettiva si ottiene tramite normalizzazione, problema che si affronterà in seguito. In conformità all'uso corrente in fisica quantistica indicheremo le ampiezze con la lettera greca ψ. Otteniamo quindi una fondamentale legge quantistica, alternativa alla (13): se un evento E può accadere tramite due processi A e B che in linea di principio non possono essere distinti attraverso un possibile esperimento, allora la probabilità dell'evento è ottenuta sommando le ampiezze (fasori) associate ai processi A e B, ed elevando poi al quadrato la lunghezza dell'ampiezza risultante.

$P (E) = {∣ψ (A) + ψ (B)∣}^{2}$

(14)

Analogamente con tre o più processi. Enunciamo quindi una fondamentale legge quantistica per la somma delle probabilità:

Fasori, ampiezze e numeri complessi: In quanto vettori bidimensionali, i fasori e le ampiezze possono essere rappresentati con numeri complessi dall'uguale intensità e fase; questa è la rappresentazione preferita dai fisici per eseguire più facilmente i calcoli, ma il metodo di Feynman rimane valido a prescindere dalla scelta di come rappresentare ampiezze e fasori.

Considereremo qui solo il caso di problemi stazionari, cioè indipendenti dal tempo. In questo caso l’angolo di fase può essere espresso dalla più semplice relazione $φ = k x$ .

Come per l'onda elettromagnetica, il numero d'onda del fotone dipende dal materiale in cui esso si sta propagando:

Nei materiali: Se il fotone non si sta muovendo nel vuoto ma in un materiale ad indice di rifrazione n, il numero d'onda diventa $k = 2 π n / λ$

Il modello di Feynman: la probabilità per un fotone emesso da una sorgente di essere rivelato da un rivelatore dipende da tutti i cammini possibili tra sorgente e rivelatore. Ad ogni cammino è associato un fasore, un vettore bidimensionale di lunghezza unitaria ed angolo di fase $φ = k x$ . Sommando tutti questi fasori si ottiene l'ampiezza, un vettore la cui intensità elevata al quadrato è direttamente proporzionale alla probabilità cercata.

2.1. Interferenza tra due fenditure con Feynman

Esaminiamo ora il problema dell’interferenza di fotoni da due fenditure usando il metodo di Feynman. Sia S la sorgente, 1 la prima fenditura, 2 la seconda fenditura. Sia d la distanza tra le fenditure, D la distanza dello schermo dalle fenditure, R il rivelatore sullo schermo (Figura 9).

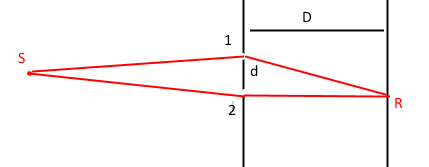
Figura 9. Schema della doppia fenditura e dei cammini possibili

Il fotone può raggiungere il rivelatore tramite due cammini: il cammino che passa per 1 e quello che passa per 2, cioè S-1-R ed S-2-R. Le ampiezze associate ai due cammini saranno rappresentate da due vettori di lunghezza unitaria (che, lo ripetiamo ancora una volta, sono “fasori” che rappresentano simbolicamente numeri complessi)

La fase associata al primo vettore è $ϕ_{1} = \frac{2 π}{λ} l_{1}$ dove l1 è la lunghezza del primo cammino, la fase del secondo è $ϕ_{2} = \frac{2 π}{λ} l_{2}$ . La differenza tra le due fasi è $Δ ϕ = \frac{2 π}{λ} Δ l$ .

Grazie a note formule trigonometriche, il quadrato del modulo della somma c di due vettori a e b con differenza di fase Df è $c^{2} = a^{2} + b^{2} + 2 a b \cos (Δ ϕ)$ . Poiché entrambi i vettori hanno lunghezza unitaria, la formula si riduce a $c^{2} = 2 + 2 \cos (Δ ϕ)$ . Assumendo che la sorgente sia equidistante dalle due fenditure, la probabilità nei vari punti dello schermo può essere trovata dalla differenza di lunghezza tra i cammini dopo le fenditure, calcolabili tramite formule trigonometriche.

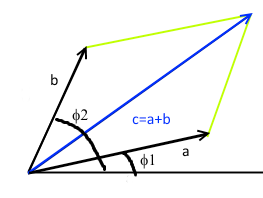
Figura 10. La somma delle ampiezze è una semplice somma vettoriale

In particolare, i massimi si avranno quando i due fasori sono paralleli, i minimi se antiparalleli:

Figura 11. Fasi reciproche delle ampiezze in condizione di massimo e minimo

Nel caso di parallelismo, $Δ ϕ$ è pari ad un multiplo intero di 2p, mentre in antiparallelismo $Δ ϕ$ è un multiplo semiintero. Una differenza tra i cammini pari ad un multiplo della lunghezza d'onda porta quindi ad un massimo, una differenza pari a metà lunghezza d'onda più un numero intero di lunghezze d'onda porta ad un minimo. I massimi si hanno quindi per:

$\begin{matrix} Δ ϕ = \frac{2 π}{λ} Δ l = 2 n π \\ Δ l = n λ (n \in Ζ) \end{matrix}$

(15)

Mentre i minimi per:

$\begin{matrix} Δ ϕ = \frac{2 π}{λ} Δ l = (2 n + 1) π \\ Δ l = (n + \frac{1}{2}) λ (n \in Ζ) \end{matrix}$

(16)

2.1.1. Approssimazione di Fraunhofer

Poniamoci ora con lo schermo molto lontano dalle fenditure, $D ≫ d$ . Sotto queste condizioni, che vengono dette di Fraunhofer, i cammini dopo le fenditure si possono considerare in prima approssimazione paralleli.

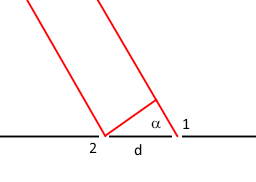
Figura 12. Condizioni di Fraunhofer: i cammini del fotone si possono considerare paralleli

Se si indica con a l'angolo formato dai due cammini che portano dalle fenditure al rivelatore con il piano delle fenditure, la differenza di lunghezza tra i cammini diventa pari a $d \sin (α)$ , e quindi la posizione dei massimi e dei minimi si trova immediatamente sostituendo nelle formule (15) e (16):

$d \sin (α) = n λ \to \sin (α) = n \frac{λ}{d}$

(17)

Per i massimi, e

$d \sin (α) = (n + \frac{1}{2}) λ \to \sin (α) = (n + \frac{1}{2}) \frac{λ}{d}$

(18)

Per i minimi. Queste posizioni corrispondono a quelle effettivamente misurate sperimentalmente.

Doppia fenditura: utilizzando il metodo di Feynman si riesce a calcolare la distribuzione di probabilità di rivelare un fotone nell'esperimento di Young con la doppia fenditura. Due cammini sono possibili per il fotone, uno per fenditura, per passare dalla sorgente al rivelatore, posto in un punto sullo schermo. La somma dei fasori associati a questi cammini porta all'ampiezza finale, il cui modulo elevato al quadrato è proporzionale alla probabilità effettivamente misurata dell'arrivo del fotone nel punto considerato.

E' possibile visualizzare il funzionamento del modello tramite la simulazione realizzata con GeoGebra (in Figura 13 oppure al link https://tube.geogebra.org/material/simple/id/efBI3J9a) dell'interferenza da doppia fenditura risolta con il metodo della somma sui cammini. L'utilizzo della simulazione non richiede l'installazione del software GeoGebra.

Figura 13. Simulazione dell'interferenza da doppia fenditura con i cammini di Feynman. E' possibile variare la distanza tra le fenditure (d), la distanza tra le fenditure e lo schermo (D) e la lunghezza d'onda del fotone incidente (lambda). La finestra di destra mostra la somma dei fasori corrispondenti ai due cammini nel punto in cui si immagina posto il rivelatore (xDetector).

2.2. Diffrazione da fenditura singola con Feynman

Si esamini ora la diffrazione da fenditura singola, sempre in condizioni di Fraunhofer per semplicità. In questo caso, non abbiamo più un numero finito di cammini, ma un cammino per ogni punto della fenditura. Il calcolo della distribuzione di probabilità esatto richiede la risoluzione di un integrale a valori complessi, ma la posizione dei minimi può essere calcolata più facilmente senza dover usare gli integrali. La Figura 14 mostra una simulazione della diffrazione da singola fenditura, disponibile anche al link https://tube.geogebra.org/material/simple/id/VljzT1uw.

Figura 14. Simulazione della diffrazione da singola fenditura con i cammini di Feynman. E' possibile variare la larghezza della fenditura (d), la distanza tra la fenditura e lo schermo (D) e la lunghezza d'onda del fotone incidente (lambda). La finestra di destra mostra la somma dei fasori corrispondenti ai due cammini nel punto in cui si immagina posto il rivelatore (xDetector).

Sia $d$ la larghezza della fenditura; consideriamo le coppie di punti della fenditura a distanza $d / 2$ l'uno dall'altro. Risulta chiaro che queste coppie di punti esauriscono tutti i punti della fenditura e che la differenza di lunghezza dei cammini che passano per tali punti è $(d / 2) \sin (α)$ . Se le ampiezze associate ad una coppia di cammini risultano antiparallele, la somma per la singola coppia è nulla, e quindi anche la somma di tutte le coppie dovrà essere nulla. La condizione di minimo diventa quindi

$\sin (α) = (n + \frac{1}{2}) (2 \frac{λ}{d}) \to \sin (α) = (2 n + 1) \frac{λ}{d} (n \in N)$

(19)

La condizione descritta individua sempre dei minimi, ma non tutti. Infatti, ad esempio, sono stati lasciati fuori dalla descrizione precedente quei minimi che corrispondono ad un angolo per cui i cammini passanti per due punti distanti $d / 3$ sulla fenditura hanno una differenza di cammino di $λ / 3$ , oppure di $2 λ / 3$ . Per trattare questo caso, si divide la fenditura in tre parti uguali, e si considerano le “triplette” di cammini corrispondenti nelle tre parti della fenditura: in questo caso i fasori formano un triangolo equilatero, e l'ampiezza risultante è ancora nulla. Generalizzando questo ragionamento è possibile derivare una condizione che include tutti i minimi di diffrazione della singola fenditura.

$\sin (α) = n \frac{λ}{d} (n \in Z, n \neq 0)$

(20)

La posizione dei massimi non può essere invece calcolata senza utilizzare il calcolo integrale. È interessante notare come posizioni sullo schermo a cui corrispondevano massimi di probabilità di rivelazione del fotone nel caso delle due fenditure a distanza $d$ , diventano invece corrispondenti a posizioni di minimo di probabilità se si aumentano le possibilità di passaggio per la luce creando una singola fenditura di larghezza $d$ ; questo è un effetto tipicamente quantistico: aumentare il numero di cammini possibili tra sorgente e rivelatore può avere l'effetto di diminuire la probabilità di trovare l'oggetto al rivelatore stesso, a seconda delle posizioni della sorgente, del rivelatore e dei nuovi cammini.

Diffrazione da fenditura singola: Si è in grado di calcolare la posizione dei minimi con il metodo di Feynman anche nel caso di diffrazione da fenditura singola. Anche in questo caso il risultato dei calcoli è in accordo con l'evidenza sperimentale.

2.3. Solo cammini rettilinei?

La formulazione originaria della fisica quantistica su cui il nostro approccio è basato si chiama “integrale sui cammini”. In questa formulazione, che usa metodi matematici molto avanzati, vengono considerati effettivamente tutti i cammini possibili (compatibili con i vincoli imposti al sistema) tra sorgente e rivelatore, compresi quelli ad esempio che percorrono strane curve, che hanno un andamento a zig-zag, e molti altri. Tuttavia, la maggior parte di tali cammini non forniscono un contributo significativo al risultato finale. Nel trasformare l'integrale sui cammini in “somma sui cammini” si fa una scelta sui cammini possibili che, se operata con attenzione, fornisce comunque il risultato corretto.

Per prima cosa, possiamo notare che si sono considerati nei calcoli precedenti solo i cammini rettilinei a tratti. Una giustificazione precisa di questa scelta richiede conoscenze di matematica ben superiori a quelle disponibili al liceo, ma una visualizzazione intuitiva può essere la seguente: la Figura 15 è tratta da una simulazione della somma di cammini per un fotone che si propaga liberamente (disponibile al link https://tube.geogebra.org/material/simple/id/qTK7gICC). Si può vedere che solo i cammini vicini alla traiettoria classica contribuiscono in modo significativo all'ampiezza finale, mentre i cammini lontani si annullano a vicenda, formando la struttura a spirale dei fasori nella metà destra della figura.

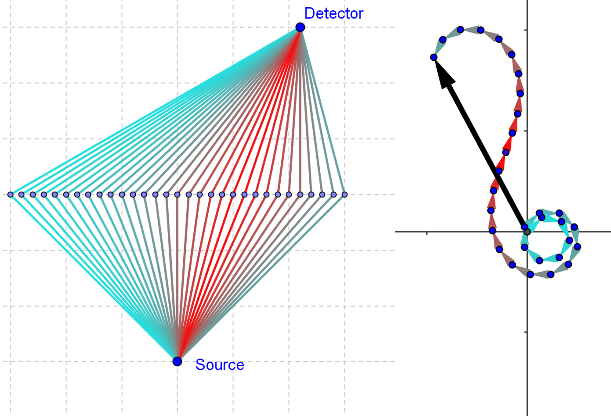
Figura 15. Screenshot di una simulazione della somma di cammini per una particella libera. I cammini sono a sinistra, i fasori associati e l'ampiezza totale a destra. I cammini, e i fasori, che maggiormente contribuiscono all'ampiezza finale hanno una colorazione tendente al rosso.

In sostanza, i cammini rettilinei a tratti sono i più importanti perché corrispondono quasi ovunque alla propagazione classica, e vengono presi come rappresentativi di molti cammini che differiscono molto poco da ciascuno di essi, che non si possono considerare nella somma e che comunque, se fossero considerati, porterebbero un contributo trascurabile.

Una seconda osservazione da fare è che i cammini da considerare devono rappresentare in modo “equo” (uniforme) tutti i cammini possibili. Anche qui, è difficile dare a questo livello una formulazione matematicamente rigorosa di questa regola, che però diventa facilmente comprensibile con degli esempi. Nella simulazione della diffrazione da singola fenditura in Figura 14 abbiamo discretizzato la fenditura in un numero finito di punti, considerando solo i cammini che, partendo dalla sorgente e arrivando al rivelatore, passavano per uno di tali punti. E' intuitivamente chiaro che, se la discretizzazione non fosse stata uniforme, ossia se ad esempio avessimo diviso la parte sinistra della fenditura in un numero di punti maggiore rispetto alla destra, il risultato ottenuto non sarebbe stato corretto. Analogamente, non sarebbe lecito per l'interferenza da doppia fenditura, con fenditure non puntiformi ma identiche, scegliere più cammini che passano per la fenditura di sinistra rispetto a quelli che passano per la fenditura di destra.

Cammini rettilinei: è giustificata la semplificazione di esaminare solamente i cammini rettilinei nell'applicazione del modello di Feynman, purchè tali cammini rappresentino “equamente” tutti i cammini possibili. I cammini che si discostano da quello rettilineo hanno fasori associati che si cancellano a vicenda, portando un contributo trascurabile o nullo all'ampiezza finale.

2.4. Effetti della riflessione

È opportuno ora introdurre una regola aggiuntiva sui cammini: l'ampiezza di un cammino di un fotone che comprende una riflessione all'interfaccia tra un mezzo ad indice di rifrazione minore ed uno ad indice di rifrazione maggiore subisce uno sfasamento di $π$ (180°) rispetto a quella calcolata tramite $φ = k x$ 1. Questo caso viene comunemente chiamato riflessione esterna.

Se la riflessione avviene in senso opposto, quindi all'interfaccia tra un mezzo dall'indice di rifrazione maggiore ad un mezzo dall'indice minore, non si ha sfasamento rispetto a quanto calcolato. Questo caso viene chiamato riflessione interna.

La trasmissione di un fotone attraverso l'interfaccia tra mezzi materiali non porta invece ad alcuno sfasamento.

Poiché la riflessione è il risultato dell'interazione luce-materia, la spiegazione di queste regole non può essere svolta senza una teoria quantistica di tali interazioni. Poiché la teoria dell'elettrodinamica quantistica è ben al di fuori del programma richiesto, limitiamoci a prendere atto di queste regole pratiche senza cercarne spiegazioni.

In Figura 16 rappresentiamo uno schema semplificato, che useremo spesso d'ora in poi per facilitare la comprensione, in cui il beam splitter sia costituito da un semplice prisma triangolare:

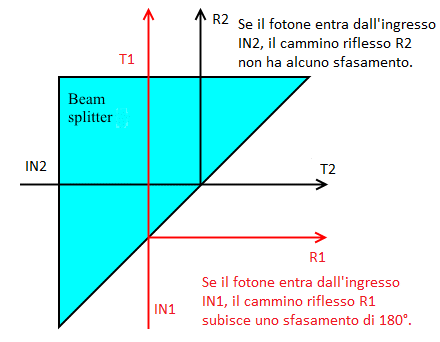
Figura 16. Schema semplificato di un beam-splitter

Come si vede dalla figura, un beam splitter può essere utilizzato come elemento base per portare cammini diversi ad interferire. Infatti, sia che il fotone entri dall'ingresso IN1, sia che entri dall'ingresso IN2, esso avrà il 50% di probabilità di uscire nelle due direzioni indicate dalle frecce. Tuttavia, la situazione vista dai due ingressi non è completamente simmetrica: infatti, se il fotone entra dall'ingresso I1, la riflessione che subisce è interna; ma se entra dall'ingresso I2, essa è esterna. Questo avrà, come vedremo nelle sezioni successive, conseguenze rilevanti nel funzionamento degli interferometri.

Effetti della riflessione: l'inclusione di una riflessione in un cammino può causare l'aggiunta di una fase di p all'angolo di fase del fasore associato. L'aggiunta di questa fase deve essere eseguita se il fotone viene riflesso da un mezzo il cui indice di rifrazione è superiore a quello del mezzo ove è presente il fotone.

2.5. Interferometro Mach-Zehnder

Un Mach-Zehnder è un apparato di interferometria ottica costituito da due normali specchi e da due beam splitter. Una sorgente emette fotoni, che sono rivelati ad una delle due possibili uscite dell'interferometro. Il Mach-Zehnder è particolarmente semplice da analizzare col linguaggio della somma sui cammini in quanto, almeno nella sua forma base, i cammini che interferiscono hanno tutti uguale lunghezza geometrica, e gli sfasamenti sono dovuti solo al diverso numero di riflessioni.

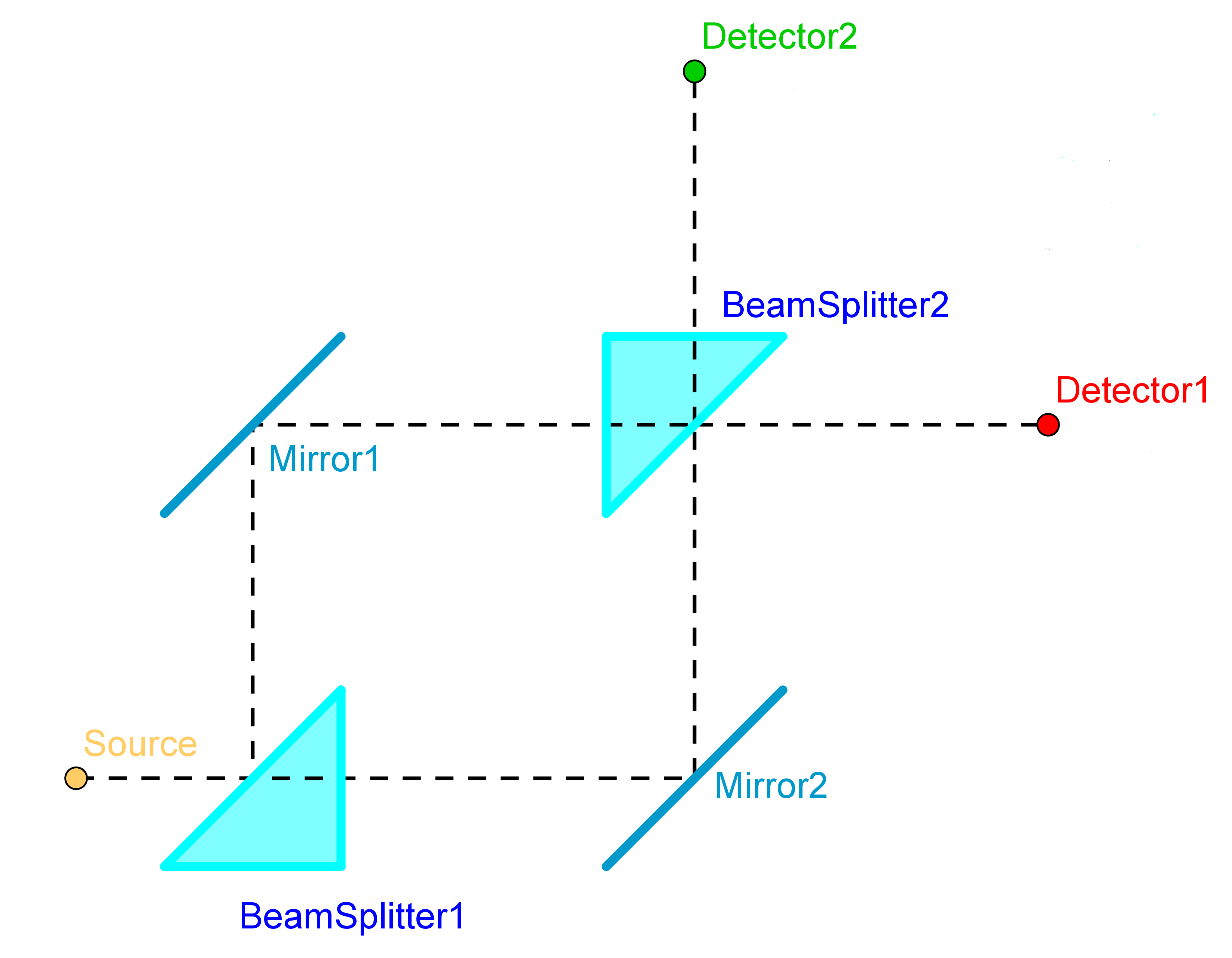
Figura 17. Schema dell'interferometro Mach-Zehnder. Le lunghezze dei due rami dell'apparato sono identiche

Si calcoli prima la probabilità che il fotone raggiunga i rivelatori se uno dei rami dell'interferometro è coperto, o se (come nelle figure seguenti) uno degli specchi è rimosso in modo da renderlo non funzionale:

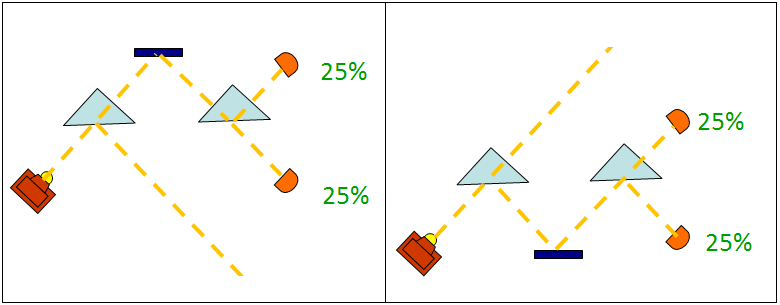
Figura 18. Il comportamento di ciascuno dei due rami del Mach-Zehnder chiudendo o eliminando l'altro.

In entrambi i casi, ad ognuno dei rilevatori arriva un solo cammino, e poiché l'ampiezza associata ai cammini è unitaria, la probabilità di rilevazione dei fotoni è uguale in entrambi i rivelatori, e quindi 25% perché metà dei fotoni originari vanno lungo il ramo che è stato disabilitato.

Se però consideriamo l'apparato nel suo complesso, ad ogni rivelatore arrivano due cammini, e quindi bisogna calcolare l'ampiezza totale risultante ad ogni rivelatore. Tutti i cammini possibili, che arrivino all'uno o all'altro rivelatore, hanno la stessa lunghezza fisica $l_{0}$ : possiamo quindi per tutti i vettori ampiezza ignorare la fase complessiva $φ_{0} = k l_{0}$ che sarà comune a tutti i cammini, e considerare solo, per ciascun cammino, gli sfasamenti ulteriori rispetto a tale fase (se rappresentiamo i vettori in un grafico, possiamo anche fissare arbitrariamente $φ_{0}$ come angolo nullo).

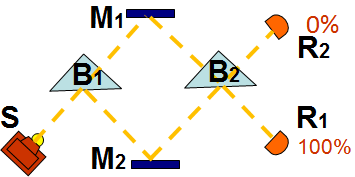
Figura 19. Il comportamento con entrambi i rami attivi.

I cammini che arrivano al primo rivelatore sono SB1M1B2R1 ed SB1M2B2R1. :

SB1M1B2R1 : Il rivelatore R1 è interessato da un cammino con trasmissione attraverso il primo beam splitter, riflessione esterna su uno specchio e trasmissione attraverso il secondo beam splitter. Il vettore associato al cammino è sfasato di p rispetto all'angolo di riferimento $φ_{0}$ che corrisponde ad un cammino di lunghezza $l_{0}$ senza riflessioni .
SB1M2B2R1 : il secondo cammino che entra nel rivelatore R1 ha una riflessione esterna sul primo beam splitter, una riflessione sullo specchio ed una riflessione esterna sul secondo beam splitter. Il vettore associato al cammino è sfasato di 3p .

I due vettori associati ai due possibili cammini hanno una differenza di fase pari a 2p, quindi sono in fase e la probabilità calcolata al rivelatore 1 è massima.

I cammini che arrivano al secondo rivelatore sono SB1M1B2R2 ed SB1M2B2R2 :

SB1M1B2R2: Il rivelatore R2 è interessato da un cammino con trasmissione attraverso il primo beam splitter, riflessione esterna su uno specchio e riflessione interna sul secondo beam splitter. Lo sfasamento sarà quindi p.
SB1M2B2R2: il secondo cammino che entra nel rivelatore R2 ha una riflessione esterna, una riflessione sullo specchio ed una trasmissione attraverso il secondo beam splitter. Lo sfasamento è 2p.

I due vettori associati ai due possibili cammini hanno differenza di fase p, sono quindi in opposizione di fase e la loro somma è il vettore nullo. La probabilità calcolata al secondo rivelatore è nulla. Nell'apparato completo, quindi, tutti i fotoni andranno nel rivelatore 1 senza mai venir rivelati dal secondo.

Il risultato è abbastanza sorprendente: infatti, dal punto di vista classico sembrerebbe ragionevole pensare che, se si effettuano, supponiamo, 50 esperimenti (emissione e rivelazione di un singolo fotone) con ciascuno dei due apparati di Figura 18, il risultato statistico dovrebbe essere uguale a quello che si ottiene nel caso in cui si effettuino 50 esperimenti con l'apparato di Figura 19; infatti al beam splitter B1 il fotone non può che essere trasmesso o riflesso, riconducendo, apparentemente, il caso di Figura 19 all'uno o all'altro dei due casi di Figura 18. Ma così non è, a causa della più importante legge della fisica quantistica: l'interferenza dei processi alternativi indistinguibili che conducono allo stesso risultato.

In altre parole, riscontriamo nuovamente quanto già visto nel caso della doppia fenditura. Se l'evento E è, ad esempio “rivelazione del fotone a R1”, la fisica classica ci direbbe che E può avvenire attraverso due possibili casi A e B (che il fotone percorra SB1M1B2R1 oppure SB1M2B2R1) fra loro mutuamente esclusivi e che hanno entrambi una probabilità del 25%, e quindi predirebbe una probabilità $P (E) = P (A) + P (B) = 50 %$ . In fisica quantistica ciò non è più vero, perché la probabilità va calcolata secondo la relazione (14) che esprime matematicamente quanto detto sopra circa l’interferenza dei processi indistinguibili.

Detto ancora in altri termini, non possiamo pensare che, nell'esperimento completo, il fotone sia passato attraverso uno solo dei due possibili bracci dell'interferometro, perché altrimenti saremmo costretti ad ammettere la validità della formula classica. Il modello del fotone che percorre tutti i cammini possibili non significa che esso percorre l'uno o l'altro di essi con una certa probabilità, ma che li “esplora” tutti contemporaneamente, in modo che essi possano interferire.

Una simulazione dell'interferometro Mach-Zehnder, che permette anche di variare la lunghezza di cammino ottico di uno dei due bracci dell'interferometro, è disponibile al link https://tube.geogebra.org/material/simple/id/NvbZqpuA.

1 Questo sfasamento è tecnicamente una “perdita” di fase, cioè la fase dopo la riflessione va diminuita, non aumentata, di $π$ . Questo dettaglio è tuttavia al momento irrilevante, anche se avrà qualche importanza nella sezione 6.